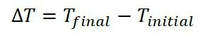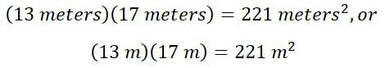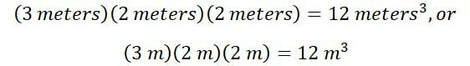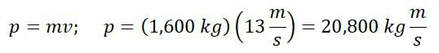"Mathematics is the Queen of Science, and Arithmetic the Queen of Mathematics." - C. F. GaussPerhaps you are thinking this module will be a waste of time: after all, you learned how to add, subtract, multiply, and divide in grade school! "What possibly could this module offer to me?" you might ask.
In the course of applying mathematics to your science coursework, you will have to use one or more of the four basic skills of arithmetic: addition, subtraction, multiplication, and division. You would be surprised to know how many students still consider these very skills to follow one set of rules in their algebra class, and yet another in science. Of prime consideration, you should know that in the world of science, figures are rarely reported without their unit counterparts. If you ask me the temperature outdoors, I would not respond merely with, "28," but rather "28 degrees Celsius." If you asked me what the difference in temperature is now, compared to two hours ago, I would still provide to you a value and unit, stating, "It is 4 degrees Celsius warmer now, than it was two hours ago." My thought process in ascertaining the temperature change can be reflected mathematically: Note whenever adding or subtracting numbers in solving problems, the units must be the same. You cannot add 4 degrees Celsius and 3 grams, because one of the units expresses temperature, and the other, mass.
When performing operations of multiplication or division, units still need to be considered. If I asked you how much turf do you need for your fenced back yard, you might figure since it is 13 meters wide and 17 meters long, you would need to multiply not only the values but the units as well: The solution of 221 meters squared expresses an area of turf needed.
If you were to ask me the capacity of our undergrown water tank, our cistern, I would similarly need to include units in this answer. Since our cistern is about 3 meters long, 2 meters wide, and about 2 meters high, I would perform the following calculation: The answer of 12 meters cubed expresses the volume of water that could be held in our cistern.
Unlike adding or subtracting units, when multiplying or dividing they need not be the same. If a 1,600 kg car ran into our fence at 13 meters per second, I could express the momentum of the car as follows: Where p is the momentum of the car, m is the car's mass in kg, and v is the car's velocity upon impact. The solution here of 20,800 kilograms times meters per second, expresses the momentum of the car as it hit our fence. Momentum is a derived unit of physics; there are countless more.
These simple examples reflect but a few of the "basic" arithmetic operations you will need to perform on numbers and units. Check-off List of Things to Do:
|
Module 1 ResourcesIn solving problems on many of the Practice Sets, you may encounter derived units you are not familiar with.
|