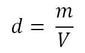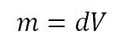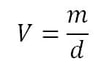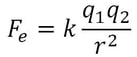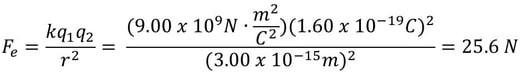“One must divide one's time between politics and equations. But our equations are much more important to me, because politics is for the present, while our equations are for eternity.” ― Albert Einstein

Often times, when solving math problems involved in the sciences, you will need to use very specific equations and formulas. Many even have names, such as Boyle's law, Charles' law, the ideal gas law, Gay-Lussac's law, law of universal gravitation, etc.

In strictly mathematical terms, a formula is an equation that relates different quantities to each other. When solving problems using formulas, you are often provided all of the known quantities for the variables, except one - which is called the unknown.

Consider the simple formula for density:
where d is density, m is the mass of the substance under investigation, and V is the volume of space it occupies. The equation enables you to learn many things: if given the mass of an object and the volume it occupies, then you can calculate density. If, however, you are trying to determine the unknown mass of an object, you can solve this knowing only the objects density and volume. In such a case the formula can be rearranged as follows, "solving" for mass:
Hopefully you are able to understand how that equation was rearranged. To isolate the variable in question (in this case, m), both sides of the equation can be multiplied by V/1. In a similar vein, if provided the density of the object and its mass, the same equation (d = m/V) can be arranged as follows in order to "solve for" volume:
Here, both sides of the original equation (d = m/V) was multiplied by V/1, and then 1/d.

Know, before you plug...

Most students agree that it is easy to plug and chug. A word of caution, however; before you plug in known variables when solving for the unknown, you must know what each of the variables stands for. As an example, consider Coulomb's law which relates the electrostatic force felt between two point charges:
Where F is the electrostatic force, q1 and q2 describe the magnitude of charges on each individual point charge, r is the distance between the two charges, and k is a constant with a value of 9.0 x 10^9 N (m^2/C^2). 

Suppose you are given this problem: "What is the magnitude of the repulsive electrostatic forces between two protons in a nucleus? Take the distance from center to center to be 3.00 x 10-15 m, and the charge of each proton is 1.60 x 10^-19 coulombs?"

Would you know how to solve this problem, given this information? If you are uncertain as to what F is, verses k, q, or r, then you are going to really struggle solving this problem. If you understand what each of the variables represents, then it's not too difficult to simply "plug" them in and solve as follows:
Do take note that not only did we calculate the numerical value of this problem, but we also employed the mathematical principles of unit cancellation so we ended up only with units of force (the newton).

So, if you are competent at rearranging the general form of equations, identifying known and unknown variables within a problem, applying mathematical principles of unit cancellation, and performing complex calculations on your calculator, you should enjoy great success in solving most of the problems you will encounter in chemistry and physics. The Professor Dave Explains videos linked right are great resources for honing many of these skills, so take the time to watch these, printing out and completing the Practice Sets as you go along.

Module 6 Resources

Check-off List of Things to Do:

  1. Read this entire webpage
  2. Watch each Professor Dave Explains video and then complete the accompanying Practice Set
  3. Check answers for each Practice Set against the Answer Key
  4. Take Module 6 Quiz